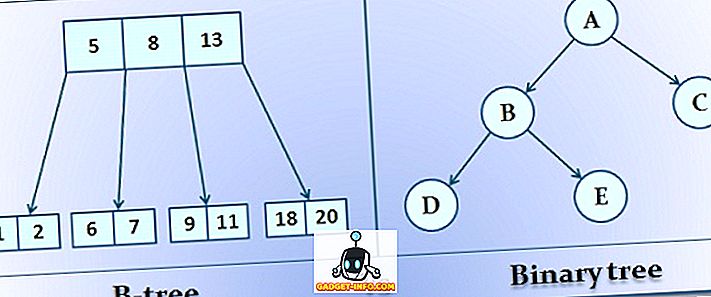
Outra diferença entre a árvore B e a árvore binária é que a árvore B deve ter todos os seus nós filhos no mesmo nível, enquanto a árvore binária não possui tal restrição. Uma árvore binária pode ter no máximo 2 subárvores ou nós, enquanto que na árvore B pode ter M não de subárvores ou nós, onde M é a ordem da árvore B.
Gráfico de comparação
| Base para comparação | B-tree | Árvore binária |
|---|---|---|
| Restrição essencial | Um nó pode ter um número M máximo de nós filhos (onde M é a ordem da árvore). | Um nó pode ter no máximo 2 números de subárvores. |
| Usava | É usado quando os dados são armazenados no disco. | É usado quando os registros e dados são armazenados na RAM. |
| Altura da árvore | log M N (onde m é a ordem da árvore M-way) | log 2 N |
| Aplicação | Estrutura de dados de indexação de código em muitos DBMS. | Otimização de código, codificação Huffman, etc. |
Definição de B-tree
Uma árvore B é a árvore M de sentido balanceada e também conhecida como árvore de ordenação balanceada. É semelhante à árvore de pesquisa binária, na qual os nós são organizados com base na passagem interna. A complexidade do espaço da árvore B é O (n). A complexidade do tempo de inserção e exclusão é O (log n).
Existem certas condições que devem ser verdadeiras para uma árvore B:
- A altura da árvore deve estar no mínimo possível.
- Acima das folhas da árvore, não deve haver subárvores vazias.
- As folhas da árvore devem estar no mesmo nível.
- Todos os nós devem ter menos filhos, exceto nós de licença.
Propriedades da árvore B da ordem M
- Cada nó pode ter um número M máximo de filhos e um número M / 2 mínimo de filhos ou qualquer número entre 2 e o máximo.
- Cada nó tem uma chave menor que as crianças com chaves M-1 máximas.
- O arranjo das chaves está em alguma ordem específica dentro dos nós. Todas as chaves na subárvore presentes à esquerda da chave são predecessoras da chave, e aquelas presentes à direita da chave são chamadas de sucessoras.
- No momento da inserção de um nó completo, a árvore é dividida em duas partes e a chave com valor mediano é inserida no nó pai.
- A operação de mesclagem ocorre quando os nós são excluídos.
Definição de árvore binária
Uma árvore binária é uma estrutura de árvore que pode ter no máximo dois ponteiros para seus nós filhos. Isso significa que o grau mais alto que um nó pode ter é 2 e também pode haver um nó de zero ou um grau.
Existem certas variantes de uma árvore binária, como árvore estritamente binária, árvore binária completa, árvore binária estendida, etc.
- A árvore estritamente binária é uma árvore na qual cada nó não terminal deve ter subárvore esquerda e subárvore direita.
- Uma árvore é chamada de Árvore binária completa quando satisfaz a condição de ter 2 nós em cada nível em que eu é o nível.
- O binário encadeado é uma árvore binária que consiste em 0 não de nós ou 2 números de nós.
Técnicas de Traversal
O traversal da árvore é uma das operações mais freqüentes realizadas na estrutura de dados em árvore em que cada nó foi visitado exatamente uma vez de maneira sistemática.
- Inorder - Nesta árvore, a subárvore esquerda é visitada recursivamente, em seguida, o nó raiz é visitado e, na última subárvore direita, é visitado.
- Preor- Nesta travessia de árvore, o nó raiz é visitado na primeira e depois na esquerda e, finalmente, na subárvore direita.
- Postorder - Essa técnica visita a subárvore esquerda, depois a subárvore direita e, finalmente, o nó raiz.
Principais diferenças entre a árvore B e a árvore binária
- Na árvore B, o número máximo de nós filhos que um nó não terminal pode ter é M, em que M é a ordem da árvore B. Por outro lado, uma árvore binária pode ter no máximo duas subárvores ou nós filhos.
- B-tree é usado quando os dados são armazenados no disco, enquanto a árvore binária é usada quando os dados são armazenados em memória rápida como a RAM.
- Outra área de aplicação para B-tree é a estrutura de dados de indexação de código no SGBD, em contraste, a árvore binária é empregada na otimização de código, codificação de huffman, etc.
- A altura máxima de uma árvore B é log M N (M é a ordem da árvore). Em contraste, a altura máxima da árvore binária é log 2 N (N é o número de nós e base é 2 porque é para binário).
Conclusão
A árvore B é usada em árvore de pesquisa binária e binária, a principal razão por trás disso é a hierarquia de memória onde a CPU está conectada ao cache com os canais de alta largura de banda enquanto a CPU está conectada ao disco através do canal de baixa largura de banda. Uma árvore binária é usada quando os registros são armazenados em RAM (pequena e rápida) e B-tree são usados quando os registros são armazenados em disco (grandes e lentos). Portanto, o uso da árvore B em vez da árvore Binária reduz significativamente o tempo de acesso devido ao alto fator de ramificação e à altura reduzida da árvore.