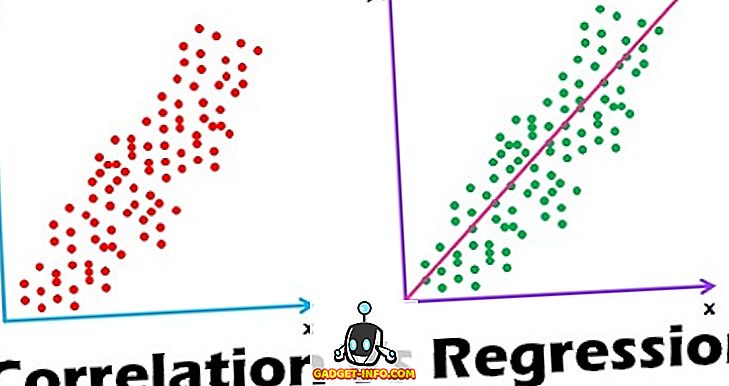
A diferença entre correlação e regressão é uma das perguntas mais comuns nas entrevistas. Além disso, muitas pessoas sofrem ambiguidades na compreensão dessas duas. Então, leia este artigo para ter uma compreensão clara sobre esses dois.
Gráfico de comparação
| Base para Comparação | Correlação | Regressão |
|---|---|---|
| Significado | Correlação é uma medida estatística que determina o co-relacionamento ou associação de duas variáveis. | Regressão descreve como uma variável independente é numericamente relacionada à variável dependente. |
| Uso | Para representar o relacionamento linear entre duas variáveis. | Para ajustar uma melhor linha e estimar uma variável com base em outra variável. |
| Variáveis dependentes e independentes | Nenhuma diferença | Ambas as variáveis são diferentes. |
| Indica | O coeficiente de correlação indica até que ponto duas variáveis se movem juntas. | Regressão indica o impacto de uma mudança de unidade na variável conhecida (x) na variável estimada (y). |
| Objetivo | Para encontrar um valor numérico que expresse a relação entre as variáveis. | Estimar valores de variável aleatória com base nos valores da variável fixa. |
Definição de Correlação
O termo correlação é uma combinação de duas palavras 'Co' (juntas) e relação (conexão) entre duas grandezas. Correlação é quando, no momento do estudo de duas variáveis, observa-se que uma mudança unitária em uma variável é retaliada por uma mudança equivalente em outra variável, isto é, direta ou indireta. Ou então, as variáveis são ditas não correlacionadas quando o movimento em uma variável não equivale a nenhum movimento em outra variável em uma direção específica. É uma técnica estatística que representa a força da conexão entre pares de variáveis.
Correlação pode ser positiva ou negativa. Quando as duas variáveis se movem na mesma direção, ou seja, um aumento em uma variável resultará no aumento correspondente em outra variável e vice-versa, então as variáveis são consideradas correlacionadas positivamente. Por exemplo : lucro e investimento.
Pelo contrário, quando as duas variáveis se movem em direções diferentes, de tal forma que um aumento em uma variável resultará em uma diminuição em outra variável e vice-versa, essa situação é conhecida como correlação negativa. Por exemplo : Preço e demanda de um produto.
As medidas de correlação são dadas abaixo:
- Coeficiente de correlação momento-produto de Karl Pearson
- Coeficiente de correlação de postos de Spearman
- Diagrama de Dispersão
- Coeficiente de desvios concorrentes
Definição de Regressão
Uma técnica estatística para estimar a mudança na variável dependente métrica devido à mudança em uma ou mais variáveis independentes, baseada na relação matemática média entre duas ou mais variáveis, é conhecida como regressão. Ele desempenha um papel significativo em muitas atividades humanas, pois é uma ferramenta poderosa e flexível que costumava prever eventos passados, presentes ou futuros com base em eventos passados ou presentes. Por exemplo : Com base em registros passados, o lucro futuro de uma empresa pode ser estimado.
Em uma regressão linear simples, há duas variáveis x e y, em que y depende de x ou digamos influenciado por x. Aqui y é chamado como dependente ou variável de critério e x é variável independente ou preditor. A linha de regressão de y em x é expressa como abaixo:
y = a + bx
onde, a = constante,
b = coeficiente de regressão
Nesta equação, aeb são os dois parâmetros de regressão.
Principais diferenças entre correlação e regressão
Os pontos abaixo, explica a diferença entre correlação e regressão em detalhes:
- Uma medida estatística que determina o co-relacionamento ou associação de duas quantidades é conhecida como Correlação. Regressão descreve como uma variável independente é numericamente relacionada à variável dependente.
- Correlação é usada para representar o relacionamento linear entre duas variáveis. Pelo contrário, a regressão é usada para ajustar a melhor linha e estimar uma variável com base em outra variável.
- Em correlação, não há diferença entre as variáveis dependentes e independentes, isto é, a correlação entre xey é semelhante a y e x. Por outro lado, a regressão de y em x é diferente de x em y.
- Correlação indica a força de associação entre variáveis. Ao contrário, a regressão reflete o impacto da mudança de unidade na variável independente na variável dependente.
- A correlação visa encontrar um valor numérico que expresse a relação entre as variáveis. Ao contrário da regressão, cujo objetivo é prever valores da variável aleatória com base nos valores da variável fixa.
Conclusão
Com a discussão acima, é evidente que há uma grande diferença entre esses dois conceitos matemáticos, embora esses dois sejam estudados em conjunto. Correlação é utilizada quando o pesquisador deseja saber se as variáveis em estudo estão correlacionadas ou não, se sim, qual a força de sua associação. O coeficiente de correlação de Pearson é considerado a melhor medida de correlação. Na análise de regressão, uma relação funcional entre duas variáveis é estabelecida de modo a fazer projeções futuras sobre eventos.