Em contrapartida, no caso de uma combinação, a ordem não tem importância. Não só na matemática, mas também na vida prática, continuamos com esses dois conceitos regularmente. Embora nunca percebamos isso. Então, leia atentamente o artigo para saber como esses dois conceitos são diferentes.
Gráfico de comparação
| Base para Comparação | Permutação | Combinação |
|---|---|---|
| Significado | Permutação refere-se às diferentes maneiras de organizar um conjunto de objetos em uma ordem seqüencial. | Combinação refere-se a várias maneiras de escolher itens de um grande conjunto de objetos, de modo que sua ordem não importa. |
| Ordem | Relevante | Irrelevante |
| Denota | Arranjo | Seleção |
| O que é isso? | Elementos ordenados | Conjuntos não ordenados |
| Respostas | Quantos arranjos diferentes podem ser criados a partir de um determinado conjunto de objetos? | Quantos grupos diferentes podem ser escolhidos de um grupo maior de objetos? |
| Derivação | Múltipla permutação de uma única combinação. | Combinação única de uma única permutação. |
Definição de Permutação
Definimos a permutação como modos diferentes de organizar alguns ou todos os membros de um conjunto em uma ordem específica. Implica toda a disposição ou rearranjo possível do conjunto dado, em ordem distinguível.
Por exemplo, toda a permutação possível criada com letras x, y, z -
- Tomando todos os três de cada vez são xyz, xzy, yxz, yzx, zxy, zyx.
- Tomando dois de cada vez são xy, xz, yx, yz, zx, zy.
O número total de permutações possíveis de n coisas, tomadas de uma vez, pode ser calculado como:
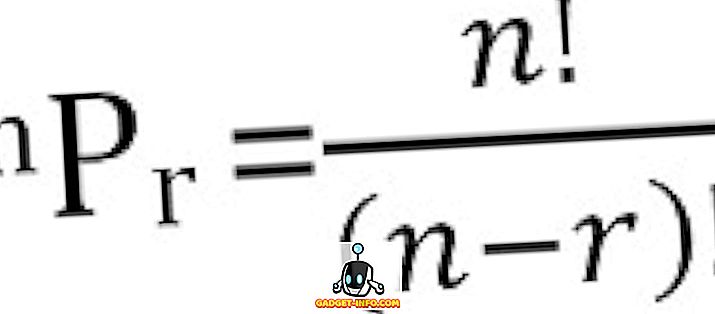
Definição de Combinação
A combinação é definida como as diferentes formas de selecionar um grupo, tomando alguns ou todos os membros de um conjunto, sem a seguinte ordem.
Por exemplo, todas as combinações possíveis escolhidas com letra m, n, o -
- Quando três de três letras devem ser selecionadas, a única combinação é mno
- Quando duas de três letras devem ser selecionadas, as combinações possíveis são mn, no, om.
O número total de combinações possíveis de n coisas, tomadas r de cada vez, pode ser calculado como:
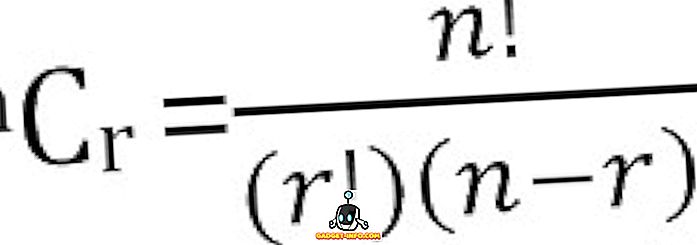
Principais diferenças entre permutação e combinação
As diferenças entre permutação e combinação são traçadas claramente pelos seguintes motivos:
- O termo permutação refere-se a várias maneiras de organizar um conjunto de objetos em uma ordem seqüencial. A combinação implica várias maneiras de escolher itens de um grande conjunto de objetos, de modo que sua ordem é irrelevante.
- O principal ponto de distinção entre esses dois conceitos matemáticos é ordem, posicionamento e posição, ou seja, em características de permutação mencionadas acima importa, o que não importa no caso da combinação.
- Permutação denota várias maneiras de organizar coisas, pessoas, dígitos, alfabetos, cores, etc. Por outro lado, a combinação indica diferentes maneiras de selecionar itens de menu, comida, roupas, assuntos, etc.
- A permutação não é senão uma combinação ordenada, enquanto Combinação implica conjuntos não ordenados ou emparelhamento de valores dentro de critérios específicos.
- Muitas permutações podem ser derivadas de uma única combinação. Por outro lado, apenas uma única combinação pode ser obtida a partir de uma única permutação.
- Respostas de permutação Quantos arranjos diferentes podem ser criados a partir de um determinado conjunto de objetos? Ao contrário da combinação que explica quantos grupos diferentes podem ser escolhidos de um grupo maior de objetos?
Exemplo
Suponha que exista uma situação em que você tenha que descobrir o número total de amostras possíveis de dois dos três objetos A, B, C. Nesta questão, primeiro de tudo, você precisa entender se a questão está relacionada à permutação. ou combinação e a única maneira de descobrir isso é verificar se a ordem é importante ou não.
Se a ordem for significativa, a questão está relacionada à permutação, e as possíveis amostras serão AB, BA, BC, CB, AC, CA. Onde, AB é diferente de BA, BC é diferente de CB e AC é CA diferente.
Se o pedido for irrelevante, a questão está relacionada à combinação e as amostras possíveis serão AB, BC e CA.
Conclusão
Com a discussão acima, é claro que permutação e combinação são termos diferentes, que são usados em matemática, estatística, pesquisa e nosso dia a dia. Um ponto a ser lembrado em relação a esses dois conceitos é que, para um determinado conjunto de objetos, a permutação será sempre maior que sua combinação.