Uma medida ideal de tendência central é aquela que é claramente definida, facilmente compreendida, simplesmente calculável. Deve basear-se em todas as observações e menos afetadas por observações extremas presentes no conjunto de dados.
As pessoas freqüentemente contrastam essas duas medidas, mas o fato é que elas são diferentes. Este artigo destaca especificamente as diferenças básicas entre média e mediana. Dar uma olhada.
Gráfico de comparação
| Base para Comparação | Significar | Mediana |
|---|---|---|
| Significado | Média refere-se à média simples do conjunto dado de valores ou quantidades. | A mediana é definida como o número do meio em uma lista ordenada de valores. |
| O que é isso? | É uma média aritmética. | É a média posicional. |
| Representa | Centro de gravidade do conjunto de dados | Centro de gravidade do conjunto de dados Ponto médio do conjunto de dados |
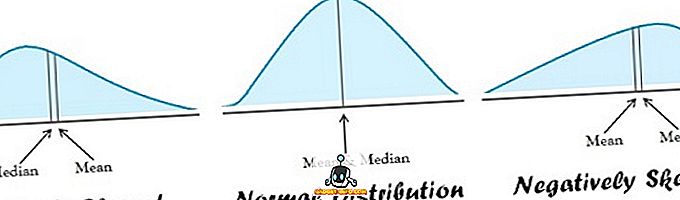
| Aplicabilidade | Distribuição normal | Distribuição enviesada |
| Outliers | A média é sensível aos outliers. | A mediana não é sensível a outliers. |
| Cálculo | A média é calculada somando todas as observações e depois dividindo o valor obtido com o número de observações. | Para calcular a mediana, o conjunto de dados é organizado em ordem crescente ou decrescente e, em seguida, o valor que cai no meio exato do novo conjunto de dados é mediano. |
Definição de média
A média é a medida amplamente utilizada de tendência central, definida como a média do conjunto de valores. Ele representa o modelo e o valor mais comum do intervalo de valores fornecido. Pode ser calculado, tanto em séries discretas quanto contínuas.
A média é igual à soma de todas as observações divididas pelo número de observações no conjunto de dados. Se o valor assumido por uma variável for igual, sua média também será a mesma. A média pode ser de dois tipos, a média da amostra (x̅) e a média da população (µ). Pode ser calculado com a fórmula dada:
- Média Aritmética :

n = número de valores - Para Séries Discretas :

- Para serviços contínuos :

A = Média Assumida
C = divisor comum
Definição de Mediana
A mediana é outra medida importante de tendência central, usada para dividir o valor em duas partes iguais, isto é, metade maior da amostra, população ou distribuição de probabilidade da metade inferior. É o valor mais intermediário, que é alcançado quando as observações são classificadas em uma ordem específica, seja em ordem crescente ou decrescente.
Para o cálculo da mediana, em primeiro lugar, organize as observações de menor para maior ou de maior para menor e, em seguida, aplique a fórmula apropriada, conforme as condições abaixo:
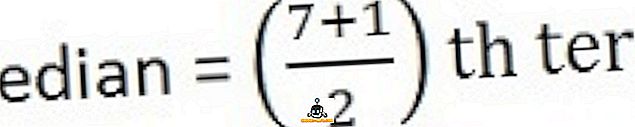
- Se o número de observações for ímpar :

- Se o número de observações for par :

- Para séries contínuas :

c = frequência cumulativa da classe mediana precedente
f = frequência da classe mediana
h = largura da classe
Principais diferenças entre média e mediana
As diferenças significativas entre média e mediana são fornecidas no artigo abaixo:
- Na estatística, uma média é definida como a média simples do conjunto dado de valores ou quantidades. A mediana é considerada o número do meio em uma lista ordenada de valores.
- Enquanto a média é a média aritmética, a mediana é a média posicional, em essência, a posição do conjunto de dados determina o valor da mediana.
- A média delineia o centro de gravidade do conjunto de dados, enquanto a mediana destaca o valor intermediário do conjunto de dados.
- A média é apropriada para dados normalmente distribuídos. No outro extremo, a mediana é melhor quando a distribuição de dados é distorcida.
- A média é altamente afetada pelo valor extremo que não está no caso de uma mediana.
- A média é calculada somando todas as observações e depois dividindo o valor obtido com o número de observações; o resultado é médio. Ao contrário da mediana, o conjunto de dados é organizado em ordem crescente ou decrescente, o valor que cai no meio exato do novo conjunto de dados é mediano.
Exemplo
Encontre a média e a mediana do conjunto de dados:
58, 26, 65, 34, 78, 44, 96
Solução: Para calcular a média, você precisa dividir a soma das observações com o número de observações,

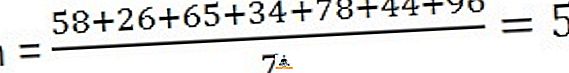
Para calcular a mediana, em primeiro lugar, organize as séries numa sequência, ou seja, da mais baixa para a mais alta,
26, 34, 44, 58, 65, 78, 96
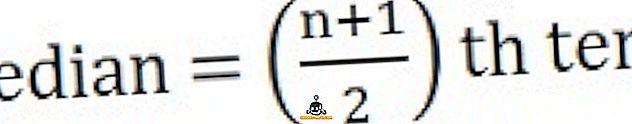
Conclusão
Depois de revisar os pontos acima, podemos dizer que esses dois conceitos matemáticos são diferentes. Média aritmética ou média é considerada como a melhor medida de tendência central, pois contém todas as características de uma medida ideal, mas tem uma desvantagem de que as flutuações da amostragem influenciam a média.
Da mesma forma, a mediana também é claramente definida e fácil de entender e calcular, e a melhor coisa sobre essa medida é que ela não é afetada por flutuações de amostragem, mas a única desvantagem da mediana é que ela não é baseada em todas as medições. observações. Para classificação de final aberto, a mediana é normalmente preferida à média.














